译自 KZG in Practice: Polynomial Commitment Schemes and Their Usage in Scaling Ethereum。
简介
零知识证明由于其数学复杂性而引发了一种神秘的气氛,它们被亲切地称为“月球数学”,因为大多数人都将它们视为超凡的魔法。
我们在 Scroll 希望能揭示零知识证明的内在运作机制。这并不会让它们失去任何神奇之处,我们认为帮助社区理解我们工作的技术层面非常重要。
在这篇文章中,我们介绍了很多零知识证明系统的关键要素:多项式承诺(polynomial commitment)方案。然后我们简要解释一下 KZG,它是实践中使用最广泛的多项式承诺方案之一。接着,我们会继续讨论如何在 Scroll 的 zk-rollups 以及以太坊的 Proto-Danksharding 中使用 KZG。最后,我们展示了 zk-rollups 以及 Proto-Danksharding 如何能够高效、优雅地相互集成,这种集成是通过它们各自使用多项式承诺方案来实现的。
为什么我们要讨论多项式?
多项式是非常强大的工具,它们在很多不同领域都有应用。 多项式可用来高效的表示大型对象。
可表示为多项式的一个标准对象是域元素 $v \isin F_p^n$ 的 $n$ 维向量。我们可以构造一个多项式 $\phi(x)$ ,通过确保 $\phi(x)$ 通过点 $(i,v_i) (i=1,2,\ldots,n)$ 来表示 $v$。
例如,我们可以将 3 维向量 $v=[2,0,6]$ 表示为多项式 $\phi(x)=4x_2−14x+12$。你可以代入值来验证确实 $\phi(1)=2,\phi(2)=0$ 和 $\phi(3)=6$ 。通过这种方式,多项式 $\phi(x)$ “编码”了向量 $v$。
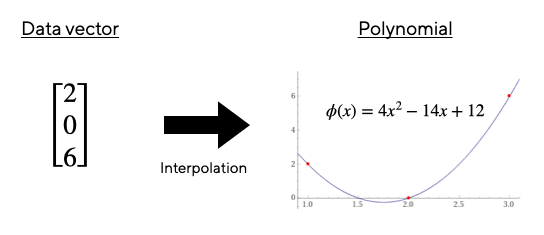
总的来说,我们可以取 $n$ 个任意点,并找到一个唯一的 $n−1$ 次多项式,使其穿过所有这些点。这个过程被称为 “多项式插值”,并且有已经建立的方法可以有效地完成这项任务。(来自 Wolfram Alpha 的巧妙 在线工具 可以根据输入的向量插值一个多项式!)
什么是多项式承诺方案?它们为何有用?
多项式承诺方案具有一些额外优点。在一般的承诺方案中,承诺者通过输出一些承诺 $c$ 来承诺信息$m$ 。然后,承诺者可随后揭示信息 $m$ ,验证者可验证承诺$c$ 对应于$m$ 。承诺方案应该是“绑定的”(一旦发布$c$ ,承诺者无法找到其他也对应于 c 的信息 $ m’ \neq m$ )和“隐藏的”(发布 $c$ 不应该揭示任何关于底层消息 $m$ 的信息)。
现在,使用多项式承诺方案,承诺者承诺的是一个多项式,而不是某个任意消息 。多项式承诺方案满足了普通承诺方案上述的属性,并且还实现了一个额外的属性:承诺者应该能够“打开”已承诺多项式的某些取值,而不需要揭示整个内容。例如,承诺者应该能够证明 $\phi(a)=b$ 而无需确切透露 $\phi(x)$ 是什么。
这是一个非常棒的属性,它对于零知识应用非常有用!我们可用它来证明我们有一些满足某些性质的多项式,而无需揭示多项式是什么。
这个属性有用的另一个原因是,承诺 $c$ 通常比它所代表的多项式要小得多。我们将看到一个承诺方案,其中任意阶的多项式可以通过其承诺表示为单个群元素。当考虑在链上发布数据时,这尤为令人期待,因为区块空间是一种宝贵的资产,任何形式的压缩都可立即转化为成本上的节约。
KZG 多项式承诺方案
好的,既然我们已经对多项式承诺方案产生了兴趣,那么让我们看看如何实际构建一个。我们将重点关注的是 Kate-Zaverucha-Goldberg (KZG) 多项式承诺方案。KZG 在区块链领域的许多任务中都得到了广泛的应用 - 它已经被 Scroll 的证明系统所使用,而且很快将与 Proto-Danksharding (EIP-4844) 一起整合到以太坊的协议中。我们稍后会详细阐述每一个用例。
这部分将简要概述 KZG 多项式承诺方案的数学构造。虽然并不全面,但应该能清楚地展示事情是如何运作的。对于喜好数学的人,我们将在本节的末尾提供一些进一步的参考资料。
无论如何,让我们从构建开始。KZG 多项式承诺方案包含四个步骤。
步骤 1:可信设置
- 首先是一次性的可信设置。一旦完成此步骤,其他步骤可以重复进行,以承诺并揭示各种不同的多项式。
- $g$ 代表某个配对友好椭圆曲线群 $G$ 的生成元。
- $l$ 代表想要承诺的多项式的最大次数。
- 随机选择域元素 $\tau \isin F_p$
- 计算 $(g,g^\tau,g^{\tau^2},\ldots,g^{\tau^l} )$ 并公开发布。
- 请注意,$\tau$ 不应被揭示 - 它是设置的秘密参数,应在设置仪式后丢弃,以便没有人能够弄清楚它的值。
译注:$g^\tau$ 是 $\tau g$的另外一种写法。
步骤 2:承诺多项式
- 给定一个多项式 $\displaystyle \phi(x)=\sum_{i=0}^l {\phi}_i x^i$
- 计算并输出承诺 $c = g^{\phi(\tau)}$
- 尽管提交者不能直接计算 $g^{\phi(\tau)}$, 因为他不知道 $\tau$,但是他可以使用设置 $(g,g^\tau,g^{\tau^2},\ldots,g^{\tau^l} )$ 的输出来计算它:$$\prod_{i=0}^l (g^{\tau^i})^{\phi_i}=g^{\sum_{i=0}^l \phi_i \tau^i} = g^{\phi(\tau)}$$
步骤三:证明取值
- 给定一个取值 $\phi(a)=b$
- 计算并输出证明 $\pi=g^{q(\tau)}$
- 此处 $q(x)=\frac{\phi(x)-b}{x-a}$,这被称为“商多项式”。请注意,只有当 $\phi(a)=b$ 时,$q(x)$ 才存在。因此,这个商多项式的存在就是取值的证明。
步骤四:验证取值证明
- 给定承诺 $c = g^{\phi(\tau)}$, 取值 $\phi(a)=b$, 证明 $\pi=g^{q(\tau)}$。
- 验证 $e(\frac{c}{g^b})=e(\pi,\frac{g^\tau}{g^a})$, 其中 $e$ 是一个 non-trivial 双线性映射。
- 一些代数学(请参阅下面的链接笔记)表明,这等同于检查步骤 3 中的属性是否在 $\tau$ 处成立:$$q(\tau)=\frac{\phi(\tau)-b}{\tau-a}$$
- 双线性映射使我们能够在不知道秘密设置参数 $\tau$ 的情况下检查此属性。
这是关于 KZG 背后的数学原理的快速概述,略去了一些细节。如果你想深入了解(并看到一个酷炫的扩展,你可以用一个证明来证明多个取值),请查看这些优秀的资源:
- Dankrad Feist’s notes on KZG 上面的证明过程与此文中相同,只是关于椭圆标量加法的记法不同。
- Alin Tomescu’s notes on KZG
使用案例
zkrollup
在 zk-rollups 的情况下,我们希望证明在 L2 上发生的某些计算是有效的。从高层次来看,L2 上发生的计算可以通过一个称为“见证生成 (witness generation)”的过程表示为一个二维矩阵。然后,该矩阵可以由一系列多项式表示 - 每一列都可以被编码为自己的一维向量。然后,计算的有效性可以表示为这些多项式之间必须满足的一组数学关系。例如,如果前三列分别由多项式 $a(x)、b(x)、c(x)$ 表示,我们可能希望关系 $a(x)⋅b(x)−c(x)=0$ 成立。多项式(代表计算)是否满足这些“正确性约束”可以通过在一些随机点上取值多项式来确定。如果在这些随机点上满足“正确性约束”,那么验证者可以断定,正确计算的概率非常高。
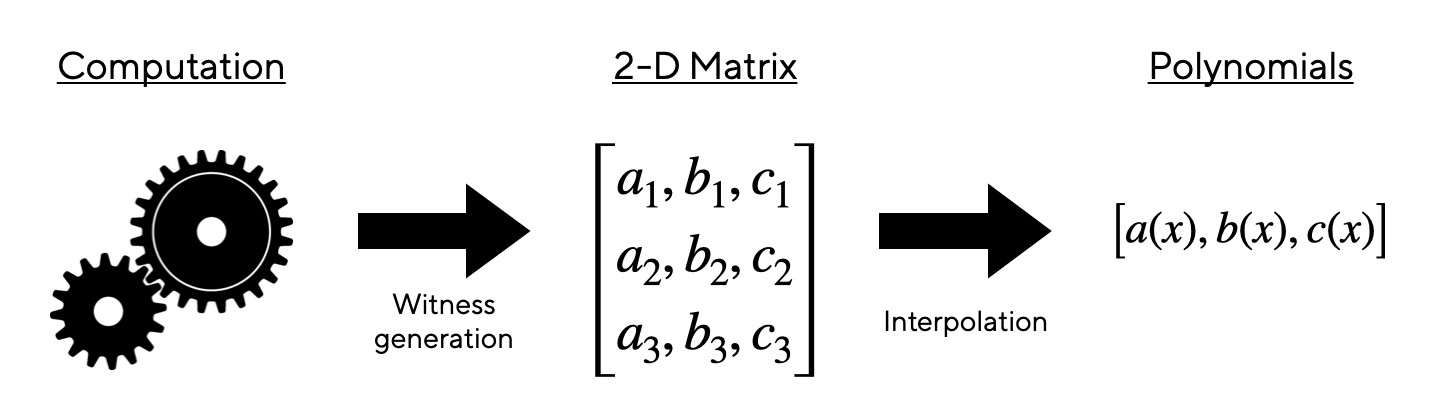
人们可以自然地看到,像 KZG 这样的多项式承诺方案如何可以直接插入到这个范例中:rollup 将承诺一组多项式,这些多项式共同代表了计算。然后,验证者可以要求在一些随机点上进行取值,以检查是否满足正确性约束,从而验证由多项式表示的计算是否有效。
Scroll 专门使用 KZG 作为其多项式承诺方案。还有一些其他的承诺方案也可以类似地运作,然而,与 KZG 相比,它们目前都有一些缺点:
Inner Product Argument (IPA) 方案具有吸引力,因为它不需要可信设置,还可以高效递归地组合。然而,它需要一个特定的椭圆曲线周期(被称为“Pasta 曲线”)才能实现其良好的递归属性。目前,以太坊并不支持在这些 Pasta 曲线上进行高效操作。这意味着在以太坊执行层进行的证明将会极其低效。如果不使用其递归属性(比如,使用非 Pasta 曲线),IPA 的证明验证时间将随电路大小线性增长,这使得它对于 zk-rollups 所需的大型电路来说不可行。
Fast Reed-Solomon IOP of Proximity (FRI) 方案也不需要可信设置。它并不依赖于椭圆曲线密码学,因此具有快速的证明生成(生成证明不需要昂贵的椭圆曲线操作),并且具有量子抗性。然而,与 KZG 相比,其证明大小和验证时间都较大。
Ethereum’s Proto-Danksharding
Proto-Danksharding(EIP-4844)是一个旨在降低 rollups 在以太坊 L1 发布数据的成本的提案。它将通过引入一种新的交易类型,即“携带数据块的交易”来实现这一目标。这种新的交易类型将携带一个较大的数据块(大约 128 kB)。然而,这个数据块将无法从以太坊的执行层访问(也就是说智能合约不能直接读取数据块)。相反,从执行层只能访问数据块的承诺。
那么,我们应该如何对数据块进行承诺呢?我们可以通过简单地对数据块进行哈希来生成一个承诺。但这有点限制性,因为我们不能在不揭示整个数据块的情况下证明其任何属性。
我们也可以将数据块视为一个多项式(请记住,将数据向量等数学对象表示为多项式是很容易的),然后使用多项式承诺方案来承诺数据。这不仅使我们能够对数据进行承诺,而且还能够有效地检查数据块的某些属性,而无需阅读整个内容。
多项式承诺方案为数据 blob 启用的一项非常有用的功能,是 数据可用性采样 (DAS)。使用 DAS,验证者可以验证数据 blob 的正确性和可用性,而无需下载整个数据 blob。我们不会深入解释 DAS 的具体工作原理,但它是由我们上面讨论的多项式承诺方案的特殊属性实现的。虽然 DAS 的实际实施并未包含在最初的 Proto-Danksharding (EIP 4844) 提案中,但它将在不久之后实施,即以太坊实现“完整” 的 Danksharding 时。
以太坊专门计划使用 KZG 作为其多项式承诺方案。研究人员已经探索了其他的多项式承诺方案,并得出结论:在短期到中期内,KZG 为以太坊的 Danksharding 路线图提供了最优雅且高效的实现。
How Scroll’s zk-rollups and Ethereum’s Proto-Danksharding interact
Scroll 的 zk-rollups 和以太坊的 Proto-Danksharding 如何互动?
我们现在已经讨论了 KZG 的两个看似独立的用途:Scroll 用它来承诺在 L2 上执行的计算,而以太坊则用它来承诺数据块。现在我们将看到这两种使用 KZG 的方式实际上可以以一种酷炫的方式互动!
在处理了一批 L2 交易并计算出新的状态根后,Scroll 将基本上向以太坊 L1 发布三件事:
- $T$ - 在 L2 上执行的交易列表。
- $s_i$ 在时间步骤 i 的新的世界状态。
- $\pi$ 证明新的世界状态 $s_i$ 有效的证据。
我们想要验证的不仅仅是新的状态根 $s_i$ 是否有效(即是否存在一些交易列表,当正确执行时,会使得之前的状态根 $s_{i−1}$ 变为新的状态根 $s_i$),而且还要验证交易列表 $T$ 实际上就是导致状态根从 $s_{i−1}$ 变为 $s_i$ 的交易列表。为了实现这一点,我们需要以某种方式强制实现 $T$ 和 $π$ 之间的联系。
$T$ 将作为数据 blob 发布,因此验证者合约将能够访问到对其的 KZG 承诺。证明 $\pi$ 本身将包含对代表计算的各种多项式的 KZG 承诺。在 $\pi$ 中承诺的一个多项式是代表已处理的交易列表的多项式。因此,我们有两个单独的 KZG 承诺对同一数据进行承诺 - 我们称它们为 $C_T$ (来自数据块)和 $C_\pi$ (来自证明),并假设它们代表同一底层多项式 $\phi_T$ (这个多项式是交易列表 $T$ 的表示)。我们可以通过“等价证明”有效地检查两个承诺是否代表同一多项式。
- 计算 $z = hash(C_T|C_\pi)$
- 发布取值证明,证明在 $C_T$ 和 $C_\pi$ 两种承诺下,$\phi(z)=a$ 都是有效的
这里的想法是选择一个随机(或类似随机)的点,然后检查两个多项式之间的等式。如果在随机选择的点上,两个多项式相等(并且点总数足够大),那么这两个多项式具有非常高的可能性是相同的。
这个等价性证明实际上适用于任何组合的多项式承诺方案 - 不管其中一个是 FRI 承诺,而另一个是 KZG 承诺,只要两者都可以在某一点打开,就没有关系。
总结
我们首先从激发多项式的兴趣开始,多项式可以轻松表示大型的数学对象。当我们引入多项式承诺方案时,它们变得更加有用。多项式承诺方案就像普通的加密承诺方案,但它具有额外的属性,即可以在不揭示整个多项式的情况下证明点取值。
然后,我们对最受欢迎的多项式承诺方案之一:KZG 进行了数学描述。该方案有四个步骤:
- 一次性的可信设置。
- 一个承诺 $c=g^{\phi(\tau)}$ 。
- 一个证明 $\pi= g^{q(\tau)}$ ,其中 $q(x)$ 是一个商多项式。
- 使用双线性映射进行验证,检查 $\phi(x)$ 和 $q(x)$ 之间的关系是否正确。
多项式承诺方案的点取值属性(point-evaluation property)使得非常酷的应用成为可能。(译注:这里的“point-evaluation property” 指的是能够有效地验证多项式在特定点上的值,而无需公开整个多项式的值。)
我们在 zk-rollups 的案例中看到了这样一个应用:计算被表示为一个多项式,通过检查多项式是否满足某些约束来验证其有效性。由于多项式承诺方案允许点取值证明,zk-rollups 可以使用简洁的承诺来代表计算,而不是使用冗长的多项式本身。
另一个应用是 Proto-Danksharding:数据块被表示为多项式,它们的承诺通过 KZG 进行计算。KZG 的数学属性使得数据可用性采样成为可能,这对于以太坊数据层的扩展至关重要。
我们最后研究了 Scroll 的 zk-rollup 证明中的承诺如何与以太坊上的数据块承诺交互。
- 虽然这听起来像是一个难以完成的任务,但是有已经建立的方法可以通过使用 多方计算(MPC) 进行这样的信任设置仪式,这些方法的信任假设较弱(1-out-of-N 信任假设)。如果你想了解更多关于信任设置如何工作的信息,请查看 Vitalik 的这篇 文章。
- 将计算过程转化为数学对象,并以数学关系表达其有效性的过程被称为“算术化”。实现这种转化的方法有很多种,但 Scroll 使用的是 Plonkish 算术化。
- 这个观点正式被称为施瓦茨-齐佩尔引理,它被广泛用于有效地验证多项式的性质。
- 请注意,这种验证器在随机点查询多项式的交互式挑战可以通过 Fiat-Shamir 变换转化为非交互式协议。
- 我们也可以通过简洁的证明来证明数据块的某些属性(例如,证明知道哈希到正确哈希的数据,然后证明该数据的某些属性),但是每次需要访问/验证数据块的信息时,这样做的成本过高。
- 从长远来看,KZG 可能需要被替换为一个抗量子攻击的多项式承诺方案。Proto-Danksharding 正在以一种方式实施,使得未来可以替换承诺方案。
- 这再次源于 Schwartz Zippel 引理。请注意,证明者在提交数据之前必须不能知道取值点 $z$ 的值 - 这将使证明者能够轻易构造一个满足$z$ 处的等式检查的伪造多项式。通过将$z$ 设置为两个承诺的哈希值,证明者在两个多项式都提交后才能知道$z$ 。
- 然而,当两个多项式承诺方案在不同的群体上运行时,会出现一个复杂问题。例如,Scroll 目前使用的是 BN254 曲线,而以太坊计划为 Proto-Danksharding 使用 BLS12-381 曲线。在这种情况下,我们无法直接比较群元素,就像上面概述的等价证明一样。然而,有一种解决方法,可以在 Dankrad Feist 的笔记中找到。


评论