Exploring Elliptic Curve Pairings

本文译自：vitalik：探索椭圆曲线配对，网上的几个译本是在不行，只能自己翻译一下。

椭圆曲线

作为各种构造背后的关键密码原语，包括确定性阈值签名、zk-SNARKs 以及其他更简单形式的零知识证明，椭圆曲线配对是其中的一种。椭圆曲线配对（或“双线性映射（Bilinear Mapping）”）是对使用椭圆曲线进行加密和数字签名的 30 年历史的最新补充；配对引入了一种“加密乘法”的形式，极大扩展了基于椭圆曲线协议的功能。本文的目的将是详细介绍椭圆曲线配对，并概述它们的工作原理的。

你不需要第一次阅读时就理解理解所有内容，甚至是第十次时，这些内容确实很难。但希望这篇文章至少能给你一点关于内部运作的概念。

椭圆曲线本身是一个非常深奥的主题，这篇文章通常假设你知道它们是如何运作的；如果你不知道，我推荐这篇文章作为入门读物：https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/（译注：也可以参考 之前的文章）。简单总结一下，椭圆曲线密码学涉及到被称为"点"的数学对象（即具有 $(x,y)$ 坐标的实际二维点），有特殊的公式用于加减它们（即计算的坐标），你也可以用一个整数乘以一个点（即 $P \cdot n = P + P + \ldots + P$ ，如果 n 很大的话，有更快的计算方法）。

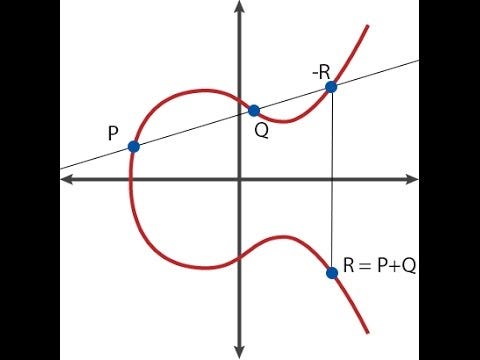
上图是点加法在图形上的呈现方式。

存在一个特殊的点，被称为"无穷远点"（ $O$ ），它在点运算中相当于零；总是满足 $P + O = P$ 。另外，一条曲线有一个"阶 (order)"；存在一个数 $n$ ，使得对任何 $P$ 都有 $P \cdot n = O$（当然，也有 $P \cdot (n+1) = P, P \cdot (7n+5) = P \cdot 5$ 等等）。还有一个被普遍接受的"生成点" $G$ ，在某种意义上被理解为代表数字 $1$ 。理论上，曲线上的任何点（除了 $O$ ）都可以是 $G$ ；重要的是 $G$ 是标准化的。

什么是配对

相比椭圆曲线的加减法，配对则更进一步，它们允许您检查椭圆曲线点上某些类型的更复杂的方程，例如，如果有 $P = G \cdot p, Q = G \cdot q, R = G \cdot r$ ，你可以检查是否有 $p \cdot q = r$ ，只需要 $P,Q,R$ 作为输入。这可能看起来像是破坏了椭圆曲线的基本安全保证，因为只知道 $P$ 就泄露了关于 $p$ 的信息，但事实证明，这种泄露是高度受限的——具体来说，决策性 Diffie Hellman 问题 是容易的，但计算性 Diffie Hellman 问题（在上述例子中，知道 $P$ 和 $Q$ ，计算 $R = G \cdot p \cdot q$ ）和离散对数问题（从 $P$ 恢复 $p$ ）仍然在计算上不可行（至少，如果它们之前是这样的话）。

观察配对作用的第三种方法，也许对我们大多数的使用案例最具启示性，那就是如果将椭圆曲线点视为单向加密的数字（即 $encrypt(p) = p \cdot G = P$ ），那么传统的椭圆曲线数学让检查数字的线性约束（例如，如果 $P = G \cdot p, Q = G \cdot q, R = G \cdot r$ ，检查 $5 \cdot P + 7 \cdot Q = 11 \cdot R$ 实际上是在检查 $5 \cdot p + 7 \cdot q = 11 \cdot r$ ），配对可以让我们检查 二次约束 (quadratic constraints)（例如，检查 $e(P,Q) \cdot e(G, G \cdot 5) = 1$ 实际上是在检查 $p \cdot q + 5 = 0$ ）。而提升到二次足以让我们处理确定性阈值签名、二次算术程序以及所有其他好东西。

那么，我们在上面介绍的这个有趣的 $e(P,Q)$ 运算符是什么呢？这就是配对。数学家有时也称之为 双线性映射；这里的"双线性"基本上意味着它满足以下约束：

$$ e(P, Q + R) = e(P, Q) \cdot e(P, R) \\ e(P + S, Q) = e(P, Q) \cdot e(S, Q) $$

请注意，+ 和 · 可以是任意的运算符；当你在创造新颖的数学对象时，抽象代数并不关心 + 和 . 是如何定义的，只要它们以通常的方式保持一致，例如 $a + b = b + a, (a \cdot b) \cdot c = a \cdot (b \cdot c)$ 和 $(a \cdot c) + (b \cdot c) = (a + b) \cdot c$ 。

如果 $P,Q,R$ 和 $S$ 是简单的数字，那么进行简单的配对就很容易：我们可以做 $e(x, y) = 2^{xy}$。然后，我们可以看到：

$$ e(3, 4+ 5) = 2^{3 \cdot 9} = 2^{27} \\ e(3, 4) \cdot e(3, 5) = 2^{3 \cdot 4} \cdot 2^{3 \cdot 5} = 2^{12} \cdot 2^{15} = 2^{27} $$

它是双线性的！

然而，这种简单的配对对于密码学来说并不适用，因为它们处理的对象是简单的整数，这些整数过于容易被分析；整数使得除法、对数计算以及各种其他计算变得容易；简单的整数没有"公钥"或"单向函数"的概念。此外，使用上述描述的配对，你可以反向操作 - 知道 $x$ ，并知道 $e(x, y)$ ，你只需进行一次除法和对数计算就可以确定 $y$ 。我们希望数学对象尽可能接近"黑箱"，你可以进行加、减、乘、除，但不能做其他任何事情。这就是椭圆曲线和椭圆曲线配对的作用所在。

如何配对

事实上，我们可以在椭圆曲线点上构造一个双线性映射——也就是说，我们可以构造一个函数 $e(P, Q)$ ，其输入 $P$ 和 $Q$ 是椭圆曲线点，输出是所谓的 $(F_p)^{12}$ 元素（至少在我们这里要讨论的特定情况下是这样；具体情况会根据曲线的细节有所不同，稍后我们会详细讨论），但是这背后的数学原理相当复杂。

素数域与扩展域

首先，让我们讨论一下素数域和扩展域。（译注：这里是为了说明配对函数设计中 $G_1,G_2,G_t$ 的域）

在这篇文章前面的图片中，那个漂亮的椭圆曲线只有在你假设曲线方程是用常规实数定义的情况下才会呈现出那样的形状。然而，如果我们在密码学中真的使用常规实数，那么你可以使用对数来“反向操作”，并且一切都会崩溃（译注：因为可以逆推出 y）；此外，实际存储和表示这些数字所需的空间可能会无限增长。因此，我们选择使用素数域中的数字。

一个素数域由一组数字 $0, 1, 2… p-1$ 组成，其中 $p$ 是素数，各种运算定义如下：

$$ a + b: (a + b) \\ a \cdot b: (a \cdot b) \\ a - b: (a - b) \\ a / b: (a \cdot b^{p-2}) $$

基本上，所有的数学运算都是在模 $p$ 下完成的（有关模运算的介绍，请参见 此处）。除法是一个特殊的情况；通常情况下，$\frac{3}{2}$ 并不是一个整数，而在这里我们只想处理整数，所以我们试图找到一个数 $x$ ，使得 $x \cdot 2 = 3$ ，其中的 . 当然是指上面定义的模乘法。多亏了 费马小定理，上面展示的指数运算技巧可以完成这个工作，但还有一种更快的方法，那就是使用 扩展欧几里得算法。假设 $p = 7$ ；以下是一些例子：

2 + 3 = 5 % 7 = 5 
4 + 6 = 10 % 7 = 3
2 - 5 = -3 % 7 = 4
6 * 3 = 18 % 7 = 4
3 / 2 = (3 * 2^5) % 7 = 5 
5 * 2 = 10 % 7 = 3

如果你多试试这种数学，你会注意到它是完全一致的，并满足所有常规规则。上述最后两个例子展示了 $(a / b) \cdot b = a$ ；你也可以看到 $(a + b) + c = a + (b + c), (a + b) \cdot c = a \cdot c + b \cdot c$，以及人们知道和喜爱的所有其他高中代数恒等式 也适用。 在现实中的椭圆曲线中，点和方程通常是在素数域中计算的。

现在，让我们来谈谈扩展域。之前可能已经见过扩展域；在数学教科书中最常见的例子就是复数域，其中实数域通过增加额外的元素 $\sqrt{-1} = i$ 进行了“扩展”。基本上，扩展域的工作方式是采用已有的域，然后“创造”一个新元素，并定义该元素与已有元素之间的关系（本例中，$i^2 + 1 = 0$ ），确保这个等式对原始域中的任何数字都不成立，并查看所有由原始域的元素和你刚刚创建的新元素的线性组合构成的集合。

我们也可以扩展素数域；例如，我们可以使用 $i$ 扩展我们上述描述的素数域 $mod 7$ ，然后我们可以进行：

$$ (2 + 3i) + (4 + 2i) = 6 + 5i \\ (5 + 2i) + 3 = 1 + 2i \\ (6 + 2i) \cdot 2 = 5 + 4i \\ 4i \cdot (2 + i) = 3 + i $$

最后的结果可能有点难以理解：我们首先将乘积分解为 $4i \cdot 2 + 4i \cdot i$，得到 $8i - 4$，然后因为我们在 $mod 7$ 数学中工作，所以变成 $i + 3$。对于除法，我们这样处理：

$$ a / b: (a * b^{p^2-2}) \% p $$

请注意，费马小定理的指数现在是 $p²$ 而不是 $p$，不过如果我们想提高效率，我们也可以扩展扩展欧几里德算法来完成这项工作。 请注意，对于该域中的任何 $x$，$x^{p^2 - 1} = 1$，因此我们将 p²-1 称为“域中乘法群的阶数”。

在实数中，代数基本定理保证了我们称之为复数的二次扩展是“完整的”——你无法进一步扩展它，因为对于你能想到的新元素 $j$ 与现有复数之间的任何数学关系（至少，由代数公式定义的任何数学关系），都能找到至少一个已经满足该关系的复数。然而，在素数域中，我们没有这个问题，所以我们可以进一步进行立方扩展（新元素 $w$ 与现有域元素之间的数学关系是一个立方方程，所以 $1,w$ 和 $w^2$ 都是彼此线性独立的），更高阶的扩展，扩展的扩展等等。而椭圆曲线配对就是建立在这种超级复数的模运算之上的。

对于那些有兴趣查看用代码编写所有这些操作所涉及的精确数学的人，这里 实现了素数域和域扩展：

配对函数标准

现在，我们来谈谈椭圆曲线配对。椭圆曲线配对（或者更准确地说，我们将在这里探讨的特定形式的配对；虽然还有其他类型的配对，但它们的逻辑相当相似）是一个映射 $G_2 \times G_1 \rightarrow G_t$ ，其中：

• $G_1$ 是一条椭圆曲线，其上的点满足形如 $y^2 = x^3 + b$ 的等式，且其中的坐标都是 $F_p$ 的元素（即，它们都是简单的数字，只是所有的算术运算都是以某个素数为模进行的）。

• $G_2$ 是一个椭圆曲线，其上的点满足与 $G_1$ 相同的方程，只是坐标是 $(F_p)^{12}$ 的元素（即，它们是我们上面谈到的超级复数；我们定义了一个新的"魔数" $w$ ，它是由 12 次多项式定义的，就像 $w^{12} - 18 \cdot w^6 + 82 = 0$ ）

• $G_t$ 是椭圆曲线结果所转化的对象类型。在我们观察的曲线中，$G_t$ 是 $\bf (F_p)^{12}$ （与 $G_2$ 中使用的同一种超级复数）。

它必须满足的主要属性是双线性，这在这个上下文中意味着：

$$ e(P, Q + R) = e(P, Q) \cdot e(P, R) \\ e(P + Q, R) = e(P, R) \cdot e(Q, R) $$

还有两个其他重要的标准：

• 高效的可计算性（例如，我们可以通过简单地取所有点的离散对数并将它们相乘来轻松配对，但这在计算上与首次破解椭圆曲线密码学一样困难，所以这不算数）
• 非退化性（当然，你可以只定义 $e(P, Q) = 1$ ，但那并不是一个特别有用的配对）

函数因子

那么我们该如何定义配对函数呢？

配对函数背后的数学原理相当复杂，涉及到的高级代数知识甚至超出了我们目前所见，但我会提供一个大纲。首先，我们需要定义因子（divisor）的概念，这基本上是表示椭圆曲线点上函数的另一种方式。一个函数的因子基本上计算了函数的零点和无穷大点（译注：这里类比多项式的因式分解，每个因式都是多项式的一个零点）。要理解这意味着什么，让我们通过几个例子来看看。让我们选定一点 $P = (P_x, P_y)$ ，并考虑以下函数：

$$ f(x, y) = x - P_x $$

译注： 理解上文中的函数 $f(x, y) = x - P_x$ 需要考虑椭圆曲线上的坐标和点的性质。在这个函数中：

1. $x$ 和 $y$ 是代表椭圆曲线上点的坐标。
2. $P_x$ 是给定的椭圆曲线上的点 $P$ 的 $x$ 坐标。它是一个已知的数值。
3. 函数 $f(x, y)$ 计算的是点 $(x, y)$ 的 $x$ 坐标与给定点 $P$ 的 $x$ 坐标 $P_x$ 之间的差值。

因子是 $[P] + [-P] - 2 \cdot [O]$ （方括号用于表示点 $P$ 出现在函数的零点和无穷大集合中，而不是点 P 本身；$[P] + [Q]$ 与 $[P + Q]$ 并不是同一回事）。推理如下：

• 该函数在 $P$ 处等于零，因为 $x$ 是 $P_x$ ，所以 $x - P_x = 0$。
• 该函数在 $-P$ 处等于零，因为 $-P$ 和 $P$ 共享相同的 坐标。
• 随着 $x$ 趋向无穷大，函数也趋向无穷大，因此我们说在 $O$ 处，函数等于无穷大。有一个技术原因需要我们将这个无穷大计算两次，所以 O 是-2 的 重数（负号是因为它是无穷远点而有别于零点，2 是因为它要被算两次）。

技术原因大致如下：因为曲线的方程是 $y^2 = x^3 + b$（译注：原文这里是 $x^3 = y^2 + b$ , 但这应该是笔误）, $y$ 向无穷大“1.5 倍速度”超过 $x$ ，以便 $y^2$ 能跟上 $x^3$ ；因此，如果一个线性函数只包含 $x$ ，那么它被表示为 $2$ 重数的无穷大，但如果它包含 $y$ ，那么它被表示为 $3$ 重数的无穷大。

译注：方括号这里只是一种特殊的数学记法，因子可以类比理解为一元高阶函数的因式分解。

现在，考虑一个"线性函数"：

$$ ax + by + c = 0 $$

在这里，$a$ 、$b$ 和 $c$ 被精心选择，以使线条通过点 $P$ 和 $Q$ 。由于椭圆曲线加法的工作方式（参见顶部的图表），这也意味着它通过 $-P-Q$ 。并且它根据 $x$ 和 $y$ 无限延伸，因此因子变为 $[P]+ [Q] + [-P-Q] - 3 \cdot [O]$。

我们知道，每一个“有理函数”（即，只通过有限数量的 + - * / 操作在点的坐标上定义的函数）唯一对应某个因子，直到乘以一个常数（即，如果两个函数 F 和 G 有相同的因子，那么 $F = G \cdot k$ 对应某个常数 k ）。

对于任何两个函数 $F$ 和 $G$ ，$F \cdot G$ 的因子等于 $F$ 的因子加上 $G$ 的因子（译注：还是类比一元多项式的因式分解）（在数学教科书中，你会看到 $(F \cdot G) = (F) + (G)$ ），所以例如如果 $f(x, y) = P_x - x$ ，那么 $(f^3) = 3 \cdot [P] + 3 \cdot [-P] - 6 \cdot [O]$ ； $P$ 和 $-P$ 被“三次计数”，以解释在某种数学意义上， $f^3$ 在这些点上“三倍速度”接近 $0$。

请注意，有一个定理表明，如果你从函数的因子中“去掉方括号”，那么这些点的总和必须等于 $O ([P] + [Q] + [-P-Q] - 3 \cdot [O]$ ，显然 $P + Q - P - Q - 3 \cdot O = O)$ 符合这个条件，而任何具有这个属性的因子都是函数的因子。

译注：这小节主要介绍了如何通过函数因子定义函数。之所以使用这种函数定义方式是为了更方便的定义函数的乘法，以及证明配对函数的双线性。

Tate 配对

现在，我们准备好来研究 Tate 配对 了。请考虑以下通过它们的因子定义的函数：

译注：$(F_P)$ 是一种特殊的记法，用于表示一个函数或数学表达式。这种记法通常在椭圆曲线密码学和相关领域中使用，用于表示特定的数学操作或计算。在这个记法中，$(F_P)$ 可以被视为一个函数或表达式的名称，

• $(F_P) = n \cdot [P] - n \cdot [O]$，其中 n 是 $G_1$ 的阶，即对于任何 P，$n \cdot P = O$ 。
• $(F_Q) = n \cdot [Q] - n \cdot [O]$
• $(g) = [P + Q] - [P] - [Q] + [O]$

现在，让我们来看看乘积 $F_P \cdot F_Q \cdot g^n$ 。因子是：

$$ n \cdot [P] - n \cdot [O] + n \cdot [Q] - n \cdot [O] + n \cdot [P + Q] - n \cdot [P] - n \cdot [Q] + n \cdot [O] $$

简化后的结果为：

$$ n \cdot [P + Q] - n \cdot [O] $$

请注意，这个因子的格式与上述 $F_P$ 和 $F_Q$ 的因子完全相同。因此，$F_P \cdot F_Q \cdot g^n = F_{P + Q}$ 。

现在，我们介绍一个被称为"最终指数化"的步骤，我们将上述函数的结果（$F_P$, $F_Q$ 等）提升到 $z = (p^{12} - 1) / n$ 的幂次，其中 $p^{12} - 1$ 是 $(F_p)^{12}$ 中乘法群的阶（即，对于任何 $x \in (F_p)^{12}, x^{(p^{12} - 1)} = 1$ ）。请注意，如果你将这个指数化应用到任何已经被提升到 $n$ 的幂次的结果上，你会得到一个提升到 $p^{12}-1$ 的幂次的指数化，所以结果变成了 $1$ 。因此，在最终指数化之后， $g^n$ 被消除，我们得到 $F_P^z \cdot F_Q^z = (F_{P + Q})^z$ 。这就是一些双线性性质。

现在，如果你想制作一个在两个参数上都是双线性的函数，你需要深入到更深奥的数学领域，在那里你不直接取一个值的 $F_P$ ，而是取一个因子的 $F_P$ ，这就是完整的“Tate 配对”来源的地方。为了证明更多的结果，你必须处理像“线性等价”和“韦伊互惠”这样的概念，而这个深渊还在继续深入。你可以在 这里 和 这里 找到更多关于这一切的阅读材料。

关于一个被修改版本的 Tate 配对的实现，称为最优 Ate 配对，请参见 此处。该代码实现了 米勒算法，这是实际计算 $F_P$ 所必需的。

请注意，像这样的事实配对是有点双刃剑：一方面，这意味着我们对所有（加密）协议可以实施配对都变得可能，但这也意味着我们必须更加小心地选择我们使用的椭圆曲线。

每个椭圆曲线都有一个被称为 嵌入度 的值；本质上，这是最小的 $k$ ，使得 $p^k -1$ 是 $n$ 的倍数（其中 $p$ 是用于该领域的素数，$n$ 是曲线的阶）。在上述领域中，$k=12$ ，而在用于传统 ECC（即我们不关心配对）的领域中，嵌入度通常非常大，以至于配对在计算上难以实现；然而，如果我们不小心，那么我们可以生成 $k=4$ 或甚至 $1$ 的域。

如果 $k=1$ ，那么椭圆曲线的"离散对数"问题（本质上，只知道点 $P = G \cdot p$ 就恢复 $p$ ，这是你必须解决的问题，以"破解"一个椭圆曲线私钥）可以被简化为在 $F_p$ 上的类似数学问题，其中问题变得更容易（这被称为 MOV 攻击）；使用嵌入度为 12 或更高的曲线确保这种简化要么不可用，要么解决配对结果上的离散对数问题至少与从公钥恢复私钥"正常方式"（即，计算上不可行）一样困难。不用担心；所有标准曲线参数都已经对这个问题进行了彻底的检查。

敬请期待即将到来的 zk-SNARKs 工作原理的数学解释。

特别感谢 Christian Reitwiessner，Ariel Gabizon（来自 Zcash）和 Alfred Menezes 的审阅和修正。

总结

这篇文章首先简单回顾了椭圆曲线的基本性质，并引出了使用配对的作用：对椭圆曲线上的点做二次约束检查或者更高级的约束。配对实际上一个双线性的映射函数。接着介绍如何构造配对函数，这个过程中首先介绍了素数域和扩展域的概念，接着介绍了椭圆曲线配对函数的构造。